From the very beginning, radio communications used Morse code for data communications. Over time, improved techniques were developed for data transmission that take into account the variability of the radio medium and greatly increase the speed at which data transmission occurs over a radio link. In addition, the application of error- correcting codes and automatic repeat request (ARQ) techniques offering error- free data transfer permits the use of radio transmissions for computer- to- computer communications systems.

To understand the principles of radio data communication, we’ll define
some common data terminology and explain the significance of the modem. We will also outline some of the problems and solutions associated with radio data communication.

Binary Data

Communication as an activity involves the transfer of information from
a transmitter to a receiver over a suitable channel. Consider this book, for instance. It uses symbols (the alphabet) to encode information into a set of code groups (words) for transmission over a channel (the printed page) to a receiver (the reader). Applying this principle to data (information), we begin by using a kind of shorthand to transform the data into code words (binary digits or bits) for transmission over a channel (HF radio) to a receiver (the reader).

Bits are part of a number system having a base of two that uses only the
symbols 0 and 1. Thus, a bit is any variable that assumes two distinct states. For example, a switch is open or closed; a voltage is positive or
negative, and so on.

A simple way to communicate binary data is to switch a circuit off and on
in patterns that are interpreted at the other end of a link. This is essentially what was done in the early days of telegraphy. Later schemes used a bit to select one of two possible states of the properties that characterize a carrier (modulated radio wave) — either frequency or amplitude. More sophisticated approaches allow the carrier to assume more than two states and hence to represent multiple bits.

Baud Rate

Data transmission speed is commonly measured in bits per second (bps).
Sometimes the word baud is used synonymously with bps, although the two terms actually have different meanings. Baud is a unit of signaling speed and is a measure of symbols per second that are being sent. A symbol may represent more than one bit.

The maximum baud rate supported by a radio channel depends on its
bandwidth — the greater the bandwidth, the greater the baud rate. The
rate at which information is transmitted, the bit rate, depends on how
many bits there are per symbol.

Asynchronous and Synchronous Data

The transmission of data occurs in either an asynchronous or synchronous
mode. In asynchronous data transmission, each character has a start and stop bit (Figure 5- 1). The start bit prepares the data receiver to accept the character. The stop bit brings the data receiver back to an idle state.

Synchronous data transmission eliminates the start and stop bits. This type
of system uses a preamble (a known sequence of bits, sent at the start of a
message, that the receiver uses to synchronize to its internal clock) to alert the data receiver that a message is coming. Asynchronous systems eliminate the need for complex synchronization circuits, but at the cost of higher overhead than synchronous systems. The stop and start bits increase the length of a character by 25 percent, from 8 to 10 bits.

Radio Modems

Radios cannot transmit data directly. Data digital voltage levels must be
converted to radio signals, using a device called a modulator, which applies the audio to the transmitter. Conversely, at the receiver, a demodulator converts audio back to digital voltage levels. The Harris radios are equipped with built- in high- speed modems (the MOdulator and the DEModulator packaged together), which permit the radios to operate with either voice or data inputs.

Radio modems fall into three basic categories: (1) modems with slow- speed
frequency shift keying (FSK); (2) high- speed parallel tone modems; and (3)
high- speed serial (single) tone modems.

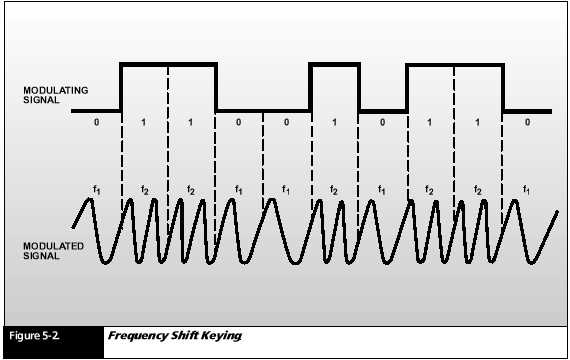
The simplest modems employ FSK to encode binary data (0s and 1s) (see
Figure 5- 2). The input to the modulator is a digital signal that takes one
of two possible voltage levels. The output of the modulator is an RF signal
that is one of two possible tones. FSK systems are limited to data rates
less than 75 bps due to the effects of multipath propagation.

Amplitude Shift Keying (ASK) is similar to FSK except that it is the amplitude of the carrier that is modulated rather than the frequency.
Higher rates are possible with more modern Phase Shift Keying (PSK)
modulation methods and advanced coding schemes. PSK is described
later in this chapter.

Error Control

There are several different approaches to avoid data transmission problems.

Forward Error Correction (FEC) adds redundant data to the data stream
to allow the data receiver to detect and correct errors. An important
aspect of this concept is that it does not require a return channel for
the acknowledgment. If a data receiver detects an error, it simply corrects
it and accurately reproduces the original data without notifying the data
sender that there was a problem. Downsides of FEC: Unlike ARQ, FEC does not ensure error- free data transmission; FEC decreases the effective data throughput.

The FEC coding technique is most effective if errors occur randomly in a
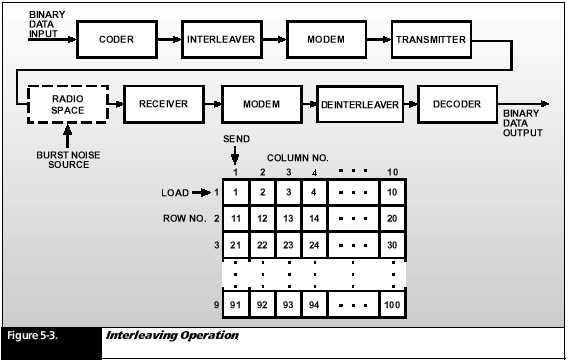
data stream. The radio medium, however, typically introduces errors that occur in bursts — that is, intervals with a high bit error ratio (BER) in the channel are interspersed with intervals of a low BER. To take full advantage of the FEC coding technique, it’s best to randomize the errors that occur in the channel by a process called interleaving (Figure 5- 3).

For example, at the modulator, the data stream enters a 9- row by 10- column matrix. The blocks are entered by rows and unloaded by columns. When the data stream leaves the matrix for transmission, the sequence of output bits will be 1, 11, 21, and so on.

At the demodulator, de- interleaving reverses the process. Data is entered
by columns in a matrix identical to that at the transmitter. It is read out in rows, restoring the sequence of data to its original state. Thus, if a burst were to cause 9 consecutive bits to be in error, no more than 3 of them will fall in any 30- bit sequence of bits after de- interleaving.

Then, if an FEC coding technique were used, the errors would be corrected.
Soft- decision decoding further enhances the power of the error- correction
coding. In this process, a group of detected symbols that retain their
analog character are compared against the set of possible transmitted
code words. The system “remembers” the voltage from the detector and applies a weighing factor to each symbol in the code word before making a decision about which code word was transmitted.

Vocoder

Data communications techniques are also used for encrypting voice calls
by a device called a vocoder (short for voice coder- decoder). The vocoder
converts sound into a data stream for transmission over an HF radio channel. A vocoder at the receiving end reconstructs the data into
telephone- quality sound.

Channel Equalization and Excision Filtering

In addition to error correction techniques, high- speed serial modems may
include two signal- processing schemes that improve data transmissions.
An automatic channel equalizer compensates for variations in the channel
characteristics as data is being received. An adaptive excision filter seeks out and suppresses narrowband interference in the demodulator input,
reducing the effects of co- channel interference, that is, interference on the same channel that is being used. Harris has patented several techniques
to perform these functions.

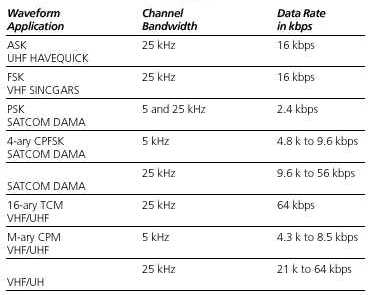
Modern High Data Rate Modem Waveforms

High- speed modem technology, permits data rates as high as 64 kbps. Radio transmission paths have varying characteristics depending upon the frequency band (HF, VHF, and UHF) and the bandwidth of the channel.
Although most HF channels are bandwidth limited to 3 kHz; VHF, UHF, and
SATCOM channels have both 5 kHz and 25 kHz bandwidths. To accommodate and maximize the data throughput rate for these radio transmission types, a number of robust data waveforms have been created. Table 5-1 lists these different waveform types and their applications.

Phase Shift Keying (PSK)

PSK is similar to FSK, shown in Figure 5- 2, except that it is the phase of the carrier rather than the frequency that is modulated.

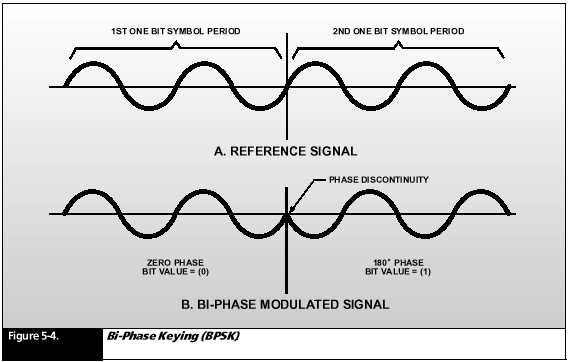
Binary Phase Shift Keying (BPSK)

The simplest form of PSK is called Binary Phase Shift Keying (BPSK) shown
in Figure 5- 4. Figure 5- 4a shows a reference wave covering two bit periods. Figure 5- 4b shows the wave after modulation with a (0) bit and a (1) bit. Notice that the signal corresponding to the second bit (1) is an upside-down version of the reference waveform. This portion of the signal is 180° with respect to the reference waveform.

Notice also that the transition from the first bit to the second is abrupt. This sudden phase discontinuity creates a burst of noise sidebands referred to as “splatter.” This noise causes inter- symbol interference which severely limits the data rate that this simple form of PSK can deliver.
M- ary PSK There are many forms of PSK. BPSK is modulated with just two phases of the carrier. Another term for BPSK is 2- ary PSK. In this case M= 2.

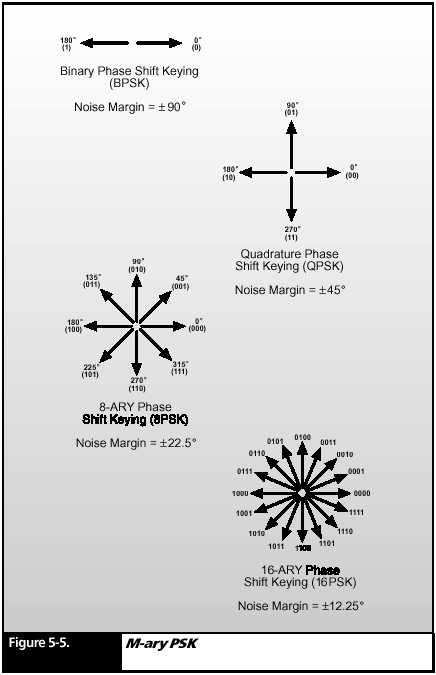
Figure 5- 5 shows a diagram that represents M- ary PSK by showing vectors that represent the phase angles associated with the most common types of
M- ary PSK modulation. BPSK is represented by two arrows facing away from each other at a 180° angle. Each of the two phases of BPSK can represent only one bit of information, either a (0) or a (1).

Quadrature Phase Shift Keying (QPSK), or 4- ary PSK, is shown with four
arrows arranged around a circle so that each is 45° apart. Since there are
four phase states used in this modulation, each of these phases can
represent two bits of information. Going clockwise around the circle,
these bits are (00), (01), (10), and (11). This multi- bit representation per phase is the key to faster data rates, because each phase represents
two bits rather than just one. The figure also shows 8- ary PSK modulation, in which each phase represents three bits. Finally, 16- ary PSK is shown. Each phase represents four bits of information. On a non- noisy radio channel, 16- ary PSK has a data rate that is four times faster than BPSK because each modulation phase state represents four times as many bits.

Continuous Phase QPSK

Figure 5- 6a shows what the waveforms of QPSK look like for each of the
four possible modulation states of (00), (10), (10), and (11). Each of these bit pairs represents a code symbol.

Figure 5- 6b shows a QPSK waveform covering two symbol periods in which
the symbols change from (00) to (10). Notice that although this requires
an 180° shift, there is no sudden discontinuity in the waveform. This is
because a transition period equal to half of the symbol period has been
taken to gradually change the phase. Although this slows down the data
rate, the extra time is made up by the decrease in discontinuity noise
(splatter) and attendant inter symbol interference.

Noise Margin

The problem with PSK waveforms with M = to 8 or 16 is that the difference
in phase between each modulation state is very small. For example, in 8- ary and 16- ary PSK, the phase difference between the (0000) and (0001)
symbols is only 45° and 22.5°, respectively. The noise margin is only half
of those values because any noise that would make the signal appear to be
half way between the true values would yield a doubtful decision. Thus the
noise margin for 8- ary and 16- ary PSK is only 22.5° and 12.5°, respectively.

In a noisy radio channel, such a narrow phase difference is much harder to
detect than the 90° noise margin of the two possible phase states in BPSK for the symbols (0) and (1). So, although 16- ary PSK can be four times as fast as BPSK in a perfect channel, it may be totally unreadable in a noisy channel.

The phase difference between adjacent phase states in a PSK scheme is
called its “noise margin”. The greater this noise margin, the more immune
to noise this symbol transition is.

BPSK may be slow, but it is very robust in a noisy channel.

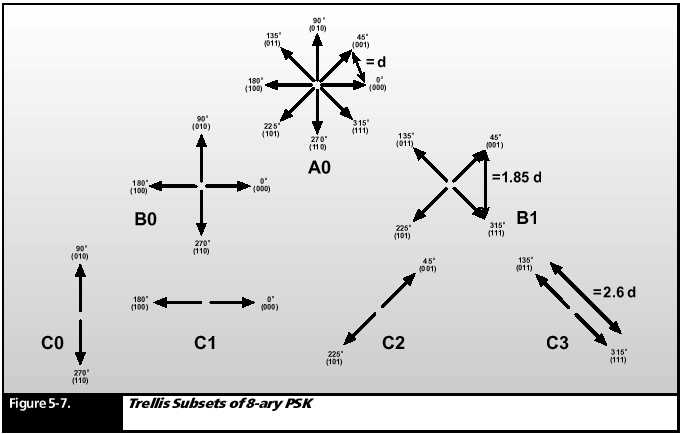
Trellis Coded Modulation (TCM)

Figure 5- 7 (A0) is a representation of an 8- ary PSK phase diagram where the linear distance between the arrows of adjacent phase points is labeled (d). As mentioned above, the noise margin corresponding to this distance is
22.5°. The term “distance” is another way of referring to noise margin.

The distance between successive symbols in a data stream can be maximized by partitioning into code subsets having increasing distance between their elements. Starting from 8- PSK constellation (in Figure 5- 7 A0), we can create two 4- PSK subsets by taking every other signal point on the circle and putting them in one set and the rest of the signal points into another set (sets B0 and B1). The distance between adjacent phases on each of these sets is 1.85 times (d).

Each of the resulting 4- PSK sets can be further partitioned into two
BPSK subsets (C0, C1, and C2, C3). The distance between the two signal
points in each BPSK subset is 2.6 times (d). Considering all combinations
of phases for each constellation, there are a total of six subsets of the
basic 8- PSK signal set.

Each choice of subset, including the choice of one of the BPSK symbols
in the last set, is assigned a bit value for a total of three bits. Because
each bit has a different signal distance associated with it, each bit has
a different likelihood of error.

The bits with the highest likelihood of error are coded into subsets with a
greater distance between bits. The effect of coding is to make the signal
different over multiple symbols due to the bit input at the present symbol.
Distance is now measured over the several symbol intervals allowing the
signal to “build up” more distance for any bit decision.

This process of subset partitioning and coding is called Trellis Coded
Modulation. This basic concept can be extended to a 16- ary PSK signal
with a bit rate of up to 64 kbps in a 25 kHz bandwidth radio channel.

SUMMARY

The transmission of data requires the use of modems to convert digital
data RF signal form when transmitting, and convert the RF signal back
to digital form when receiving.

Radio modems are classified as slow- speed FSK, high- speed parallel
tone, or high- speed serial tone.

Serial tone modems provide vastly improved data communications,
including a higher data rate with powerful forward error correction
(FEC), greater robustness, and reduced sensitivity to interference.
FEC systems provide error correction without the need for a return link.

Interleaving is a technique; mostly used for HF channels that
randomizes error bursts, allowing FEC systems to work more effectively.

Soft- decision decoding further reduces bit error rates by comparing a
group of symbols that retain their analog character against the set of
possible transmitted code words.

A vocoder converts voice signals into digital data for coded
transmission over HF channels.

Automatic channel equalization and adaptive excision filtering are
signal processing techniques that improve data communications
performance.

M- ary Phase Shift Keying is a method of increasing the data rate of
radio transmissions. “M” refers to the number of phases used in the
modulation scheme.

Trellis Coded Modulation (TCM) is a coding technique that provides
maximum data rate capability to PSK data streams by improving the
noise margin.